浅析如何灵活运用卖出期权

　本文以铜期权为例，从统计学的角度去说明，持之以恒地选择适当的期权合约，在适当的时机卖出，将是一种长期占优的投资策略。

　　无数投资者初次接触期权时，都会听到一句话，“期权买方损失有限，收益无限”。这句话指的是期权买方至多损失全部权利金，而一旦看对方向，获益的上限极大。由于这种特性，对普通投资者而言，买期权的吸引力似乎远远高于卖期权。然而，本文中，笔者将以铜期权为例，从统计学的角度去说明，卖出期权实际上是一种长期占优的投资策略。

　　盘整行情中，选择卖出期权占优

　　有一个基本逻辑是，如果一笔投资可能盈利100元，也可能亏损10元，但亏损的概率是95%，它的预期收益是-4.5元，则这是一笔价值极低的投资。以CU1912C48000期权为例，在2019年10月16日某时刻的价格为240元，标的期货合约价格为46820元，隐含波动率10.51%，30日历史波动率为7.43%。此时，如果卖出该期权，投资者能够获得一个正的预期收益，那么这就是一项值得投资的策略。

　　作为期权卖方，确定的收入是240元/吨的权利金，未来的赔付额则取决于CU1912合约从当前时刻至11月25日的涨幅。显然，当CU1912合约涨至48000以上时，期权卖方需要赔付买方。假设CU1912合约价格为x，则需要赔付x-48000元。那么，从统计的角度讲，P(x>48000)（期货价格涨至48000以上的概率）是多少呢？此例中，期权隐含波动率是10.51%，期货30日历史波动率是7.43%，则估计的未来29个交易日沪铜的累积涨跌幅的标准差应该是10.51%÷×=3.58%，或者7.43%÷×=2.53%。我们可以近似地认为CU1912合约未来29个交易日的累积涨跌幅服从一个正态分布N(0，3.58%)，或者N（0，2.53%）。

　　CU1912合约价格超过48000需要上涨逾2.52%，在N(0,3.58%)正态分布假设下，该概率为24.07%，即期权卖方有约24%的可能性需要赔付买方。当CU1912合约价格超过48240时，期权卖方将会进入亏损区间，在N(0,3.58%)正态分布假设下，该概率为19.84%。因此，从胜率的角度看，期权卖方获利的可能性超过8成，胜率较高。

　　尽管期权卖方胜率较高，但考虑到卖方亏损的空间较大，存在“一次亏损抵消数次盈利”的可能，因此，简单地从高胜率的角度判定卖期权能够稳定获利是不恰当的。从前文描述中可知，期权卖方最终的盈利由期初权利金收入和期末赔付额决定。在期货合约价格x大于48000时，卖方需要赔付，赔付额是x-48000，而x的概率密度函数为，其中φ(3.58%)是均值为0，标准差为3.58%的正态分布概率密度函数。由于沪铜期货价格不是连续变化的，我们可以通过黎曼和近似地求解卖方需要赔付的预期值，计算公式为 ，计算结果为238元，近似地等于权利金。

　　上述结果并非巧合。它的内在逻辑是，如果CU1912合约的年化波动率是10.51%，那么期权卖方的预期收益接近0，完全符合公允定价的逻辑。但是投资者需要注意的是，隐含波动率并非真实的波动率，而是对远期波动率的预期，且通常情况下都高于历史波动率，如下图所示：

虚值期权的保证金约3250元/吨，则此项投资的预期收益率约为4.3%，预期年化收益率约40%。" src="https://file.xuetz.com/upload/image/2019-10/1571627467907039500.jpg" align="middle" style="margin: 0px auto 19px !important; padding: 0px; border: 0px; vertical-align: middle; max-width: 550px; height: auto; display: block;"/>

　　在此例中，CU1912过去30日年化波动率仅为7.43%，如果未来一个月波动率基本持平，则预期赔付额大幅降低至99.4元/吨，期权卖方的预期收益从前者的2元/吨变成140.6元/吨。由于卖出该虚值期权的保证金约3250元/吨，则此项投资的预期收益率约为4.3%，预期年化收益率约40%。

　　从上述分析可知，如果标的资产未来的波动率不存在较大的变化，卖出期权的策略能够获得一个统计意义上较稳定的预期投资收益。

　　波动率合适时，卖出虚值期权

　　基于上述例子做进一步思考。假设未来30日标的期货合约波动率降至5%，则预期赔付额降至24.5元/吨，期权卖方的预期收益升至215.5元/吨，则预期收益率约为6.6%，年化收益率约为60%。更极端的情况是波动率降至0，则期权买方的年化收益率是67.6%。细心的读者已经发现，期权卖方的预期收益率与远期波动率具有一定的负相关关系。

看涨期权的预期收益率和预期波动率的关系与普通卖出看涨期权的收益曲线非常类似。事实上，卖出看跌期权的预期收益率和预期波动率的关系亦与上图一致。" src="https://file.xuetz.com/upload/image/2019-10/1571627468016060848.jpg" align="middle" style="margin: 0px auto 19px !important; padding: 0px; border: 0px; vertical-align: middle; max-width: 550px; height: auto; display: block;"/>

　　从上图可以看出，卖出看涨期权的预期收益率和预期波动率的关系与普通卖出看涨期权的收益曲线非常类似。事实上，卖出看跌期权的预期收益率和预期波动率的关系亦与上图一致。

　　换言之，无论是卖出看涨期权，还是卖出看跌期权，实际上都等同于卖出远期波动率。需要特别注意的是，由于期货价格的急涨急跌都会使波动率上升，因此，波动率的变化只是影响预期收益。从统计的角度看，假设投资者进行了成千上万次卖权投资，远期波动率走弱会使其获得正收益，远期波动率走强则使其收益减少，并随着波动率的继续上升而陷入亏损。一言以蔽之，波动率走强不利于期权卖方，波动率走弱则利于期权卖方。因此，投资者想要通过卖出期权获得稳定的盈利，最重要的不是去判断价格走势，而是分析波动率的变化趋势。

　　结合上文得出的一个显而易见的结论，即卖权的预期盈亏平衡点是远期波动率等于期权隐含波动率，卖出期权应该选择一个隐含波动率高于历史波动率的期权。此时，隐含波动率高于历史波动率的部分就成为投资策略的安全边际。

　　另一个点是，期权隐含波动率与执行价格之间有一个普遍的关系，即“波动率微笑曲线”，对于同一个标的资产，执行价与标的现价越远的期权对应的隐含波动率越高。下图是CU1912合约各执行价的看涨期权在10月16日的隐含波动率，呈现出明显的“微笑曲线”特征。结合前文的分析，投资者应该卖出距离标的现价较远的期权，由此可以获得较大的安全边际和较高的胜率。

实值期权具有明显的保证金优势，在同等绝对收益额的情况下，拥有更高的收益率。所以，期权卖方的优先选项是虚值期权。" src="https://file.xuetz.com/upload/image/2019-10/1571627468120012845.jpg" align="middle" style="margin: 0px auto 19px !important; padding: 0px; border: 0px; vertical-align: middle; max-width: 550px; height: auto; display: block;"/>

　　考虑到卖出期权需要缴纳保证金，且保证金是A）期权合约结算价+标的期货合约交易保证金-（1/2）×期权虚值额和B）期权合约结算价+（1/2）×标的期货合约交易保证金中的较大者，因此，虚值期权较实值期权具有明显的保证金优势，在同等绝对收益额的情况下，拥有更高的收益率。所以，期权卖方的优先选项是虚值期权。

　　以CU1912合约为例，10月17日某时刻，30日历史波动率7.21%，执行价分别为47000—51000元/吨的看涨期权的价格分别为425、174、69、25、14元。投资者卖出以上期权的预期收益率与波动率的关系如下图所示：

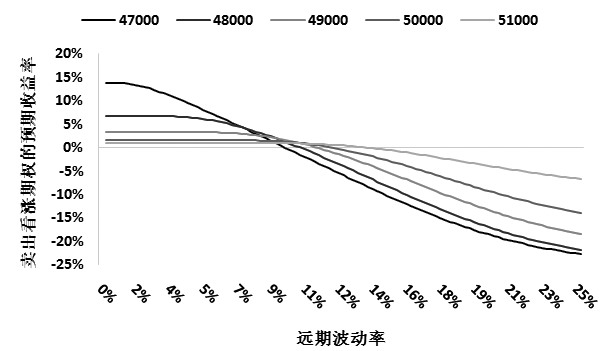
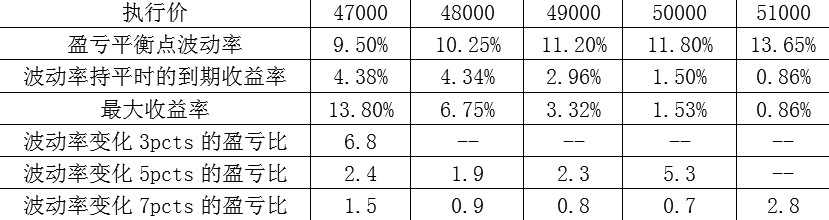
　　首先，高执行价期权隐含波动率更高，卖出期权获得正收益的区间更广；其次，卖出低执行价期权可以获得更高的潜在收益，也可能遭受更大的潜在损失；最后，从盈亏比（最大盈利/最大亏损）来看，低执行价期权似乎更占优势。

　　猛一看上述图表，卖出CU1912C47000似乎是最佳选择，但事实上并非如此。我们首先考查波动率。CU1912此时的30日历史波动率是7.21%，为近一年的低位，未来继续下降的可能性和空间都非常小，回升的可能性则比较大。因此，卖出CU1912C47000期权的预期收益率上行概率较小，下行概率较大。其次，我们观察到卖出执行价为47000和48000的看涨期权在波动率持平时所能获得的预期收益率非常接近。因此，综合思考后，卖出CU1912C48000或许是一个更优的策略。更保守的投资者甚至可以选择CU1912C49000，也能拥有一不错的预期收益。

　　选择入场时机，获取安全边际

　　期权价格是由期权的内在价值和时间价值决定的。实值期权内在价值为正，虚值期权内在价值为零。期权价格中扣除内在价值的部分即为时间价值。因此，实值期权的价格中包含内在价值和时间价值两部分，而虚值期权的价格中只包含时间价值。

　　时间价值会随着期权到期日的临近而衰减至零。因此，前文所有的策略中，期权卖方都主要是在赚取时间价值。我们以期货欧式看涨期权为例，它的理论定价c=Se-qtN(d1)-Ke-rtN(d2)。那么，时间价值=Se-qtN(d1)-Ke-rtN(d2)-max(S-K,0)。理论中，我们有一个Theta值来衡量期权价格相对时间的变化，即，是期权价格对时间的偏微分函数。利用简单的数理知识即可知，Theta也等于?时间价值/?t。换言之，期权价格相对时间变化的变化值实际上就是时间价值相对时间变化的变化值。

　　通常情况下，我们取，表示时间每减少一单位，时间价值会减少多少。理论上，针对实值、平值、虚值的三种情况，Theta曲线如下所示：

　　横轴是日期，右端是行权日。图中曲线表明，在距离行权日较远时，时间价值变化较缓慢；在行权日前一个月，平值期权时间价值将会开始迅速下降；在行权日前15天，实值和虚值期权的时间价值变化速率将会迅速放缓。原因在于，时间价值实际上代表的是期权的博弈价值，随着剩余时间的减少，虚值期权和实值期权的博弈价值已经非常低。如下图所示，虚值和实值期权的时间价值会提前逾一个月衰减至一个较低的水平，而此时接近平值的期权仍具有较高的时间价值。

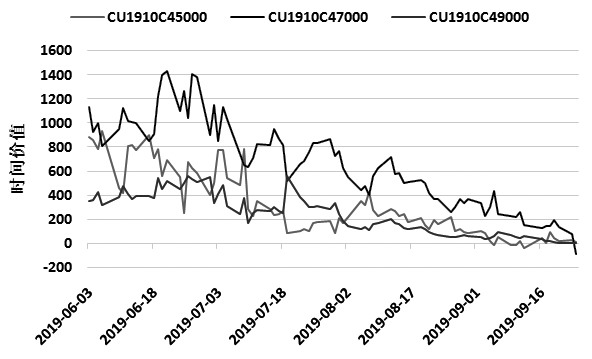
　　由于卖出期权主要是在赚取时间价值，那么，时间价值衰减得越快，卖方的资金使用效率将越高。前文已有结论，接近平值的期权在行权日前一个月的时间内，其时间价值将开始加速衰减。但是由于接近平值，内在价值可能大幅上升，从而给期权卖方带来巨大不确定性。因此，如果要卖出接近平值的期权，应该将内在价值的变化对冲掉，即通过构建资产组合对冲掉头寸中的Delta值和Gamma值。本文主要讨论简单的卖权投资，所以不对对冲策略做更多论述。

　　我们以虚值期权为例，来讨论期权卖方最合适的入场时机。研究发现，虚值额较大的期权，时间价值衰减的速率随时间的推进日益降低。虚值额越小的期权，时间价值的最大衰减日期就越接近行权日。例如，标的价格47000元/吨，行权价49000元/吨的沪铜看涨期权，时间价值衰减最快的日期约在行权日前倒数第60个日历日，而行权价48000元/吨的看涨期权，时间价值衰减最快的日期约在行权日前倒数第15个日历日。实测数据分析发现，CU1910C48000的最大Theta值出现在9月16日，CU1909C48000则出现在7月19日。实测结果与理论结果略有差异，但总的来说，卖出虚值额较大的期权应该尽早入场，卖出虚值额越小的期权，应选择相对越晚的时间。

　　第一部分的讨论告诉我们，卖出期权并不是“豺狼虎豹”，实际上是一种统计意义上的胜率较高且预期收益为正的稳定投资策略，尤其是在标的资产方向不明的时候。

　　第二部分的讨论结果是，卖出期权实际上等同于卖出一个波动率看涨期权，即沽空波动率。一方面，沽空波动率的所带来的收益不是线性的，投资者需要选择一个较高的波动率卖出，以获得较高的安全边际；另一方面，若卖出的波动率过高，实际的预期收益率会大幅降低。因此，在考虑保证金的情况下，期权卖方的最佳选择是隐含波动率相对适中的虚值期权。

　　第三部分的讨论表明，期权卖方的收益主要来自时间价值的衰减，且对于虚值期权而言，时间价值衰减最快的时刻随着虚值额的减小而愈发接近行权日。因此，卖出期权应该根据所选期权的虚值额灵活决定入场时机，以获得最大的资金利用效率。